Page 6 - loading... please wait :)

‫‪6‬‬

‫חלק ראשון של השיעור ‪ -‬מדדים‪:‬‬

‫לאחר שהבנו איך הטבלאות ייראו (בהמשך נתחיל לפתור תרגילים)‪ ,‬הדבר הבא שנלמד זה מדדים‪.‬‬
‫אלו יהיו השאלות בבחינה‪ ,‬כאשר בכל סעיף יבקשו מאיתנו לחשב מדד אחר‪ .‬נתחיל‪:‬‬

‫מדד – מספר כלשהו המסכם את חישוב של נתוני המדגם (כלומר חישוב של התצפיות במדגם)‪.‬‬
‫למדדים יש ‪ 3‬קבוצות עיקריות‪:‬‬

‫‪ -‬מדד מיקום מרכזי – ערך כלשהו שסביבו מרוכז חלק ניכר מתצפיות המדגם (למשל ממוצע)‪.‬‬

‫‪ -‬מדד פיזור – מידה כלשהי שחושבה המתארת את פיזור התצפיות ביחס למדד מיקום מרכזי‬

‫(למשל סטיית תקן)‪.‬‬ ‫‪-‬‬
‫מדד מיקום יחסי – מידה כלשהי שחושבה המתארת מיקום של תצפית מסוימת ביחס לכל‬

‫התצפיות (למשל העשירון העליון – מייצג את ה‪ 10% -‬הכי גבוהים מתוך ה‪ 100% -‬של המדגם)‪n.‬‬
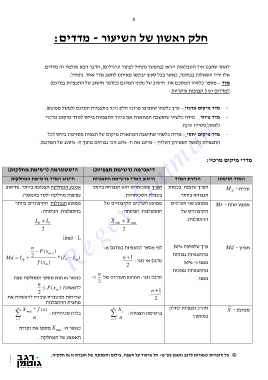
‫היסטוגרמה (רשימת מחלקות)‪tma‬‬
‫חישוב המדד ברשימת המחלקות‬ ‫מדדי מיקום מרכזי‪:‬‬

‫אמצע המחלקה הצפופה ביותר‪( .‬חישוב‪u‬‬
‫צפיפות מחלקה ילמד בהמשך)‪.‬‬
‫ממוצע הגבולות הקיצוניים ביותר‪G‬‬
‫בהתפלגות‪ .‬הנוסחה‪:‬‬
‫דיאגרמה (רשימת תצפיות)‬ ‫הגדרת המדד‬ ‫המדד וסימונו‬
‫הערך שנצפה בכמות‬ ‫שכיח ‪M O -‬‬
‫חישוב המדד ברשימת התצפיות‬
‫הערך ששכיחותו היא הגבוהה ביותר‬ ‫הגבוהה ביותר‪.‬‬ ‫אמצע טווח ‪Mr -‬‬
‫ממוצע שני הערכים‬
‫בטבלת השכיחויות‪.‬‬
‫ממוצע הערכים הקיצוניים של‬ ‫הקיצוניים של‬
‫ההתפלגות‪.‬‬
‫ההתפלגות‪ .‬הנוסחה‪:‬‬

‫‪X min  X max‬‬
‫‪2‬‬
‫‪vL0  L1‬‬
‫‪e2‬‬
‫‪egMd‬‬ ‫‪limit - L‬‬

‫‪n‬‬ ‫) ‪ F (xm1‬‬ ‫לפי מספר התצפיות במדגם ‪:n‬‬ ‫ערך שלפחות ‪50%‬‬ ‫חציון ‪Md -‬‬
‫‪2‬‬ ‫) ‪f (xm‬‬ ‫מדגם אי זוגי‪n  1 :‬‬ ‫מהתצפיות גבוהות‬
‫כאשר ‪ m‬הוא מספר המחלקה שבה‪R‬‬‫‪‬‬‫‪L0‬‬‫‪‬‬‫‪* (L1‬‬‫‪‬‬‫) ‪L0‬‬ ‫‪2‬‬
‫ממנו ו‪50% -‬‬
‫מדגם זוגי‪ :‬ממוצע הערכים של ‪ n‬ו‪-‬‬ ‫מהתצפיות נמוכות‬
‫‪2‬‬
‫‪. n1‬‬ ‫ממנו‪.‬‬
‫‪2‬‬
‫‪n‬‬ ‫‪‬‬ ‫) ‪F(xm‬‬ ‫לראשונה‬
‫‪2‬‬
‫שכיחות מצטברת עוברת לראשונה את‬
‫מחצית ההתפלגות‬

‫בלוח שכיחויות‪n X mid * f (x) :‬‬ ‫ברשימת תצפיות‪n X i :‬‬ ‫סה"כ תצפיות לחלק‬ ‫ממוצע ‪X -‬‬
‫במספרן‪.‬‬
‫‪i1 n‬‬ ‫‪i1 n‬‬

‫כאשר ה‪ X mid -‬מסמן את נקודת‬
‫האמצע של המחלקה‪.‬‬

‫© כל הזכויות שמורות לרגב גוטמן בע"מ‪ -‬חל איסור על הפצה‪ ,‬צילום והעתקה של חוברת זו או חלקיה‪.‬‬